Esempio di regressione (seconda parte)

Ricapitolando

Nell’ultimo articolo avevo introdotto un caso di studio sulla regressione. Avevo ottenuto risultati discreti utilizzando SVR. Ora voglio proporvi un metodo che riesce ad ottenere risultati nettamente migliori.

Di cosa sto parlando?

Le reti neurali, di tipo MLP (Multi Layer Perceptron). Per trattare il problema in esame ho quindi usato una rete neurale MLP adatta per la regressione.
Prima di vedere i risultati ottenuti voglio fare una breve introduzione tecnica sull’uso e sul funzionamento di questo metodo.

Funzionamento

La tipologia di rete MLP è una sottoclasse delle reti neurali artificiali. Una rete neurale artificiale cerca di imitare il funzionamento del cervello umano. È composta da neuroni (come rappresentato in figura 1), il cui numero varia ad ogni livello della rete. I neuroni sono inizialmente inizializzati con valori randomici, poi nel corso dell’allenamento del modello variano per adattarsi ai dati dei training.
In figura 1, la rete rappresentata ha 3 neuroni in input, 4 nel secondo livello (nascosto) e 2 in output.

Figura 1 - esempio di rete neurale. Immagine sotto licenza CC BY-SA 3.0. URL.

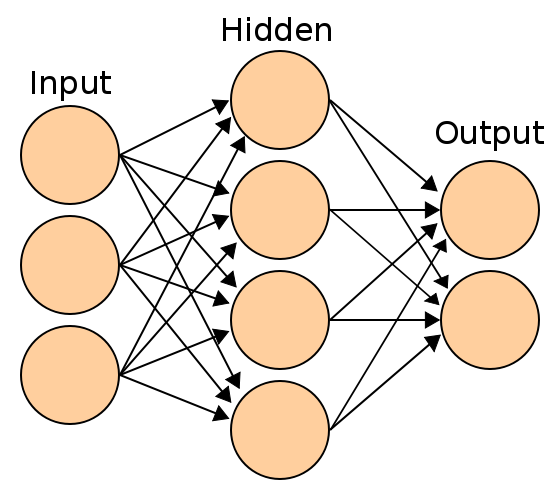
Nello specifico, la rete neurale cerca di ridurre l’errore fra risultato ottenuto e valore atteso (ground truth), modificando i pesi dei vari neuroni.

Funzione di loss

Tramite il calcolo e l’uso di una funzione di loss. Nel caso di studio analizzato, le loss valutate saranno due: MSE loss e MAE loss. Ho utilizzato queste due loss perché sto trattando un problema di regressione. Nel caso, avessi trattato un problema di classificazione non le avrei neanche prese in considerazione.

Come progettare la rete (i vari livelli) e il numero di neuroni?

Anche in questo caso la capacità e l’esperienza del data scientist è di vitale importanza.
In questo caso specifico, ho utilizzato una rete neurale con 4 neuroni per l’ input (x1, y1, x2, y2) e 2 neuroni per l’output (xc, yc). Il numero di neuroni nell’hidden layer è pari a 100.
Ho allenato la rete per 500 epoche.

Teorema di approssimazione universale

Perché utilizzare le reti neurali per risolvere il problema in esame?
Per via del teorema di approssimazione universale.
“Afferma che una rete con un singolo strato nascosto può approssimare qualsiasi funzione continua, ma non da alcuna indicazione su come ottenerla, come istruirla e se un singolo strato sia la scelta più efficiente.”
Come sempre ho utilizzato la versione delle artificial neural network proposta da sklearn.

Figura 2 - immagini del test set. Il punto blu rappresenta il centro del quadrato calcolato tramite la formula del punto medio, mentre il punto verde rappresenta il risultato predetto dalla rete neurale.

Risultati

Visto? Risultati decisamente interessanti! La rete è riuscita ad imparare a predire correttamente nelle varie situazioni il punto centrale del quadrato. Se analizziamo la MAE possiamo notare che l’errore medio su entrambe le coordinate è di circa 0.3 pixel. Rispetto ai risultati ottenuti con SVR nell’ articolo precedente, la rete neurale ottiene risultati decisamente migliori.
Come mai, utilizzando le reti neurali, MSE è minore di MAE?
Essendo le discrepanze molto piccole (minori di 1), il quadrato di questo valore sarà ancora più piccolo.

Homepage

Federico Magliani

Sono appassionato di Intelligenza Artificiale e nel 2020 ho ricevuto il Ph.D. in Visione Artificiale presso l'Università degli Studi di Parma. Se vuoi ricevere maggiori informazioni sull'articolo o sui progetti che sto svolgendo visita il mio sito web. Privacy Policy