Esempio di regressione
by Federico Magliani
Ricapitolando
Nei problemi di regressione, l’obiettivo è quello di determinare un valore continuo avendo a disposizione solo valori continui. È quindi differente dal problema di classificazione, in cui dobbiamo decidere se ogni istanza appartiene alla classe 1, alla classe 2, .. alla classe N.
Problema
In questo articolo voglio proporre un semplice problema di regressione. Dati in input il vertice sinistro alto e il vertice destro basso di un quadrato, voglio calcolare il centro dello stesso. Il mio dataset è composto da 450 istanze di dimensioni 400x400. Utilizzerò 400 istanze per il training del modello e 50 per il test. In ogni istanza del dataset ho variato randomicamente: dimensioni del quadrato, ascissa del primo punto e ordinata del secondo punto. Ho realizzato una gif con le immagini delle istanze del training set per aiutare nella comprensione del problema.

Procedimento adottato
Per risolvere il problema ho adottato l’algoritmo SVR, che è la versione dell’algoritmo di classificazione SVM idoneo a risolvere i problemi di regressione. Ho utilizzato la versione dell’algoritmo disponibile nella libreria python sklearn.
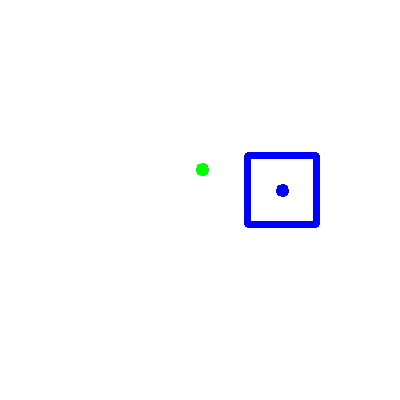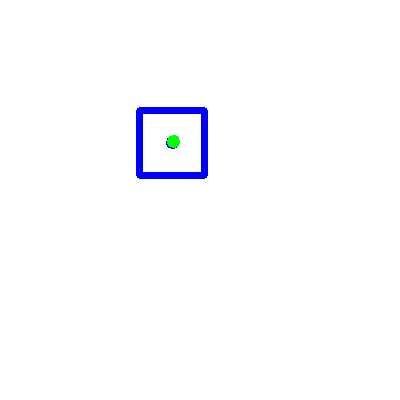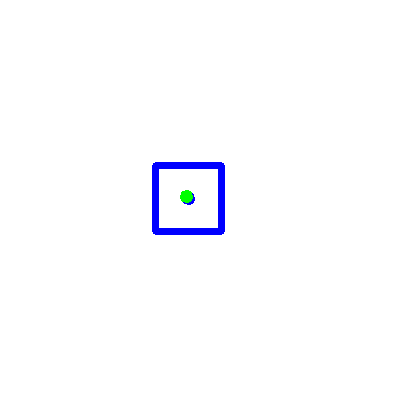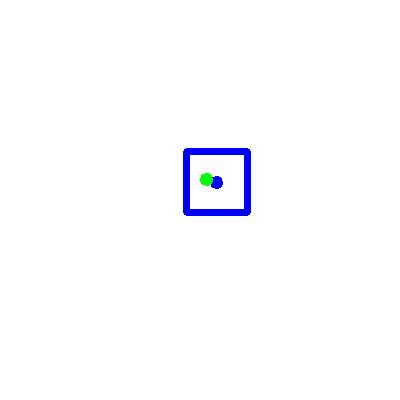
Ho quindi testato il mio metodo sulle istanze del test set. Inserisco l’immagine dei risultati ottenuti. Il punto verde indica la predizione svolta dal SVR, mentre il punto blu indica il ground truth calcolato tramite la formula del punto medio.
Nota bene
Il ground truth indica per ogni istanza del dataset le coordinate del punto da trovare. Senza queste informazioni non sarebbe possibile allenare e successivamente testare il modello di regressione.
Esempio di groun truth:
- TRAIN - Square 0 Point A 199 112 Point B 273 186 Center point 236 149
- TRAIN - Square 1 Point A 71 135 Point B 123 187 Center point 97 161
- TRAIN - Square 2 Point A 108 205 Point B 189 286 Center point 148 246
- TRAIN - Square 3 Point A 127 96 Point B 196 165 Center point 162 130
- TRAIN - Square 4 Point A 60 134 Point B 147 221 Center point 104 178
- TRAIN - Square 5 Point A 77 40 Point B 135 98 Center point 106 69
- …
Il punto A è sempre quello in alto a sinistra, mentre il punto B è sempre quello che si trova in basso a destra.
Per valutare la qualità del modello proposto ho utilizzato due indicatori comuni: Mean Squared Error e Mean Absolute Error.
Definizioni
- Mean Squared Error: indica la discrepanza quadratica media fra i valori dei dati osservati ed i valori dei dati stimati (da Wikipedia). Tende ad aumentare significativamente all’aumentare della differenza fra valore calcolato dall’algoritmo e valore del ground truth.
- Mean Absolute Error: indica la media fra i valori dei dati osservati ed i valori dei dati stimati. Tende a crescere meno significativamente rispetto al MSE all’aumentare della differenza fra valore calcolato e valore del ground truth.
Risultati

Visto che devo determinare sia l’ascissa che l’ordinata del punto centrale del quadrato avrò quindi un errore distinto per entrambi i campi. I risultati ottenuti come si può evincere anche visivamente sono discreti, ma non eccellenti. Considerando che le immagini hanno dimensione 400x400 e il MAE è di circa 23 pixel allora l’errore medio è circa il 6%.
Nel prossimo post vi spiegherò come fare per migliorare questo risultato, raggiungendo errori che tendono allo zero. Non perdetevi il prossimo post!

Federico Magliani | Sono appassionato di Intelligenza Artificiale e nel 2020 ho ricevuto il Ph.D. in Visione Artificiale presso l'Università degli Studi di Parma.
Se vuoi ricevere maggiori informazioni sull'articolo o sui progetti che sto svolgendo visita il mio sito web. Privacy Policy |